Ya sabemos la definición de ángulo, ¿pero cómo medimos los ángulos? En este curso vamos a ver una de las distintas formas que existen de medir ángulos, que son los grados sexagesimales.

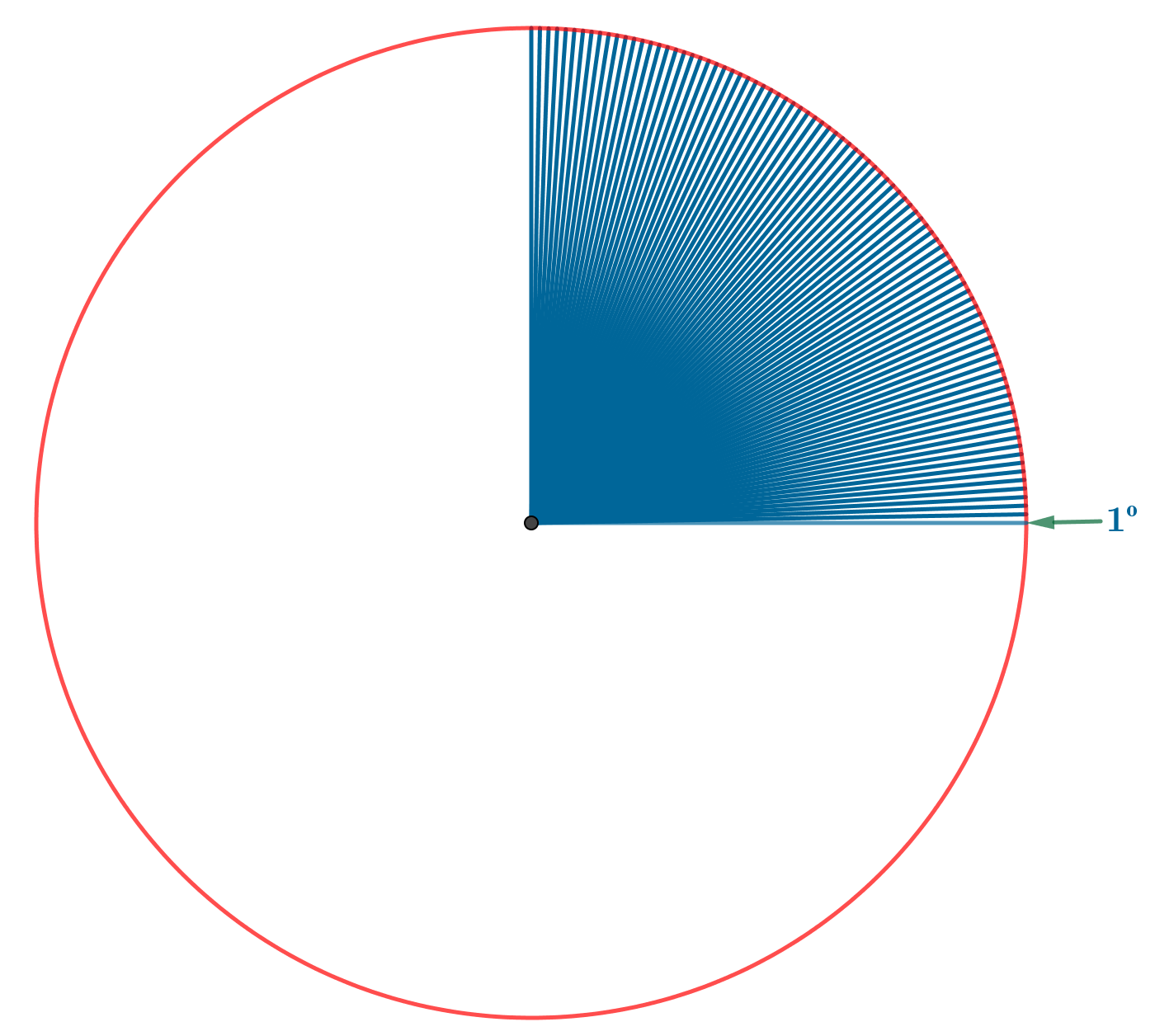
Un grado sexagesimal es la amplitud de cada uno de los ángulos que dividen a una circunferencia en 360 partes iguales.

Un grado sexagesimal es el medida de un ángulo central de una circunferencia cuyo arco de circunferencia correspondiente es la 1/360 parte de la longitud de la circunferencia.

Un ángulo recto tiene 90º sexagesimales y un ángulo llano tiene 180º sexagesimales.

Un grado sexagesimal, a su vez, se puede dividir en 60 partes iguales, cada parte se llama  minuto y cada minuto tiene 60 segundos.

Un ángulo se puede expresar en varias unidades, forma compleja, o en una sola unidad, forma incompleja (decimal).
\[15^{\circ}\,30'=15,5^{\circ}\]

El angulo $34^{\circ}\,21'\,12''$ se lee: "34 grados 21 minutos y 12 segundos'".

Para transformar un ángulo en forma compleja a forma decimal se dividen los minutos por 60, los segundos por 3600 y se suman a los grados.

Para transformar un ángulo en forma decimal a forma sexagesimal se separa la parte entera, que serán los grados de la parte decimal; la parte decimal se multiplica por 60, la parte entera del resultado serán los minutos y la parte decimal se multiplica por 60 para obtener los segundos.